Location - Finding the closest location and and sorting records by distance, based on the current location of the user
Given a data source that contains a list of locations how do we find the record
that matches the location nearest to where the user currently is? Also, how can we sort the records in a data source by the relative distance?
In this post, we'll walk through the formula that enables us to carry out this task
Demonstration of technique
To demonstrate this technique, let's take a map of the following underground stations. The latitude and longitude values are as follows:Bayswater 51.512254, -0.187522
Queensway 51.510473, -0.186959
Lancaster gate 51.511721, -0.175290
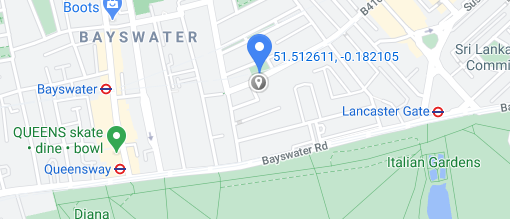
Let's now assume that we're at the given co-ordinate:
51.512611, -0.182105
How do we find the closest underground station, and return a list of the stations sorted in terms of relative distance?
Setting-up our source data
In this example, we'll use the following collection as a data source. In practice, we could data from a SharePoint list or any other data source.
ClearCollect(colLocations,
{StationName:"Bayswater", StationLat:51.512254, StationLong:-0.187522},
{StationName:"Queensway", StationLat:51.510473, StationLong:-0.186959},
{StationName:"Lancaster Gate", StationLat:51.511721, StationLong:-0.175290}
)
Building a formula to calculate and to sort records by distance
To carry out the distance calculation, we apply the Haversine formula that I described in my earlier post here.
We call the AddColumns function to add a column called "Distance" to our data source. We use the Haversine formula to caulate the relative distance between the static input coordinate, and the coordinates from the data source.
We can then apply the SortByColumns function around the return value of AddColumns to return the records sorted by distance ascending order. Here's our final formula.
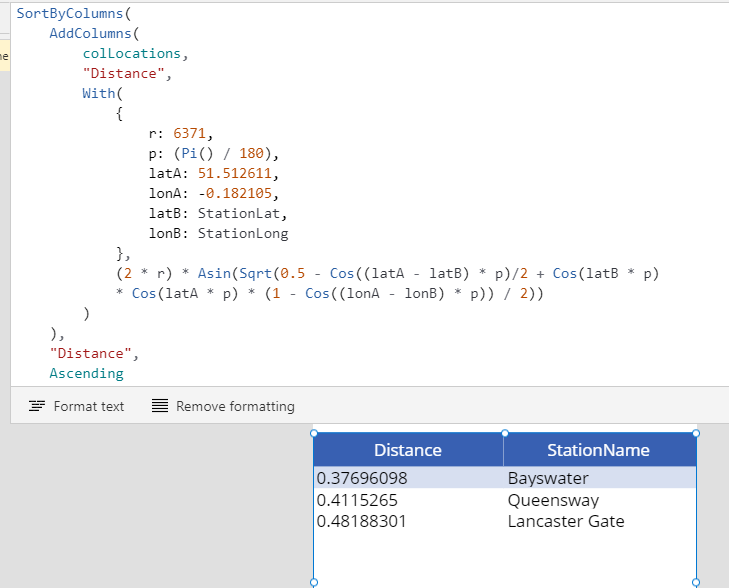
SortByColumns(
AddColumns(
colLocations,
"Distance",
With(
{
r: 6371,
p: (Pi() / 180),
latA: 51.512611,
lonA: -0.182105,
latB: StationLat,
lonB: StationLong
},
(2 * r) *
Asin(Sqrt(0.5 - Cos((latA - latB) * p)/2 + Cos(latB * p) *
Cos(latA * p) * (1 - Cos((lonA - lonB) * p)) / 2))
)
),
"Distance",
Ascending
)
Here, latA and lonA refer to the input coordinate. We can substitute this as required, or substitute these values with calls to Location.Latitude and Location.Longitude to return the current location of the user.
Testing this formula
To test this formula, the screenshot beneath shows the result when we set the items property of a data table to this formula. As we can see, the closest underground station is Bayswater, with a distance of 0.3km.
Conclusion
In this post, we looked at how to apply the Haversine formula to return a list of records, sorted by the distance relative to an input coordinate.
