Blog

Formulas - How to calculate the distance between 2 points

We can calculate the distance between two longitude and latitude co-ordinates using a trigonometric calculation. It's a complex formula so in this post, we'll find out how exactly this works, including a verification of the result. We'll see how to perform this distance calculation in both kilometers and miles.

A question that arises occasionally is - how do I to calculate the distance (as the crow flies) between two points, based on longitude and latitude values?

A search for this question frequently return example formulas that mostly derive from a formula that Keith Whatling shares in his video beneath. I recommend watching this video.


This calculation contains a complex trigonometric equation. Whilst we can simply copy and paste the logic, it always makes good sense to understand how a formula works.

Therefore in this post, we'll examine more closely the maths behind this equation.

What's the methodology behind this technique?

The methodology behind this technique relies on something called the Haversine formula. Wikipedia's article offers the following the succinct description – the "haversine formula determines the great-circle distance between two points on a sphere given their longitudes and latitudes”.

 
In simple terms - to measure the distance between two points on Earth, we must apply a trigonometric function to account for the variance that the curvature of the Earth causes.

The Wikipedia and other mathematical based articles provide a full explanation of haversine formula but for our purposes, we can distil it down to the following pseudocode. 

lat1 = <latitude value of point A>
lon1 = <longitude value of point A>
lat2 = <latitude value of point B>
lon2 = <longitude value of point B>

r = 6371 #radius of Earth (KM)
p = 0.017453292519943295  #Pi/180
a = 0.5 - cos((lat2-lat1)*p)/2 + cos(lat1*p)*cos(lat2*p) * (1-cos((lon2-lon1)*p)) / 2

d = 2 * r * asin(sqrt(a)) #2*R*asin
The code above refers to the latitude and longitude of points A and B, expressed as lat1, lon1, lat2, and lon2.

The final value d, represents the distance between points A and B in kilometers.

There is also a dependency on two constants:
  • p = pi divided by 180 degrees
  • r = the approximate radius of the Earth (6371 km)

How to calculate the distance with Power Apps

Taking our pseudocode, we can now build a Power Apps implementation of the formula. To demonstrate, we'll calculate the distance between London and Manchester:
 
  • London = Latitude: 51.509865,   Longitude: -0.118092
  • Manchester = Latitude: 53.483959,   Longitude: -2.244644

With(
    {
        r: 6371,
        p: (Pi() / 180),
        latA: 51.509865,
        lonA: -0.118092,
        latB: 53.483959,
        lonB: -2.244644
    },
    (2 * r) * 
    Asin(Sqrt(0.5 - Cos((latA - latB) * p)/2 + Cos(latB * p) * Cos(latA * p) * 
    (1 - Cos((lonA - lonB) * p)) / 2))
)

Verifying our result

To provide some verification of our result, we'll compare our calculation against the result of an online calculator. We'll use the site that Keith mentions:
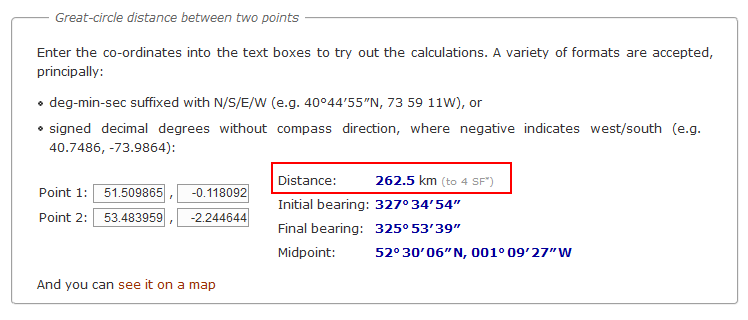
This indicates a distance of 262.5km.

Our formula in Power Apps produces the same result.


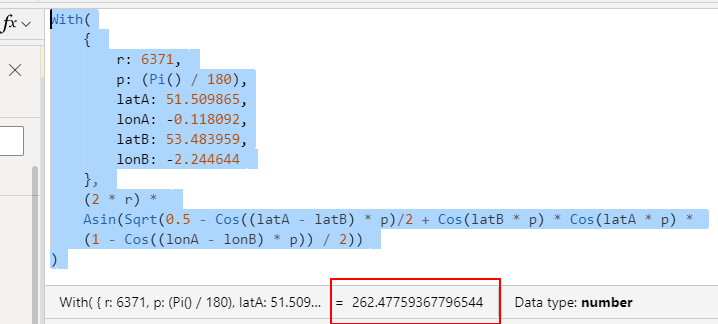
Refinements - Rounding the Distance to 2 decimal places

Taking our base formula, we can adapt it as required. A typical requirement is to round the value, and we can do this by calling the round function like so:

//Distance between 2 points in kilometers to 2 decimal places
With(
    {
        r: 6371,
        p: (Pi() / 180),
        latA: 51.509865,
        lonA: -0.118092,
        latB: 53.483959,
        lonB: -2.244644
    },
    Round(
         (2 * r) * 
            Asin(Sqrt(0.5 - Cos((latA - latB) * p)/2 + Cos(latB * p) * Cos(latA * p) * 
            (1 - Cos((lonA - lonB) * p)) / 2)),
         2
   )
)

How to calculate the distance between 2 points in miles

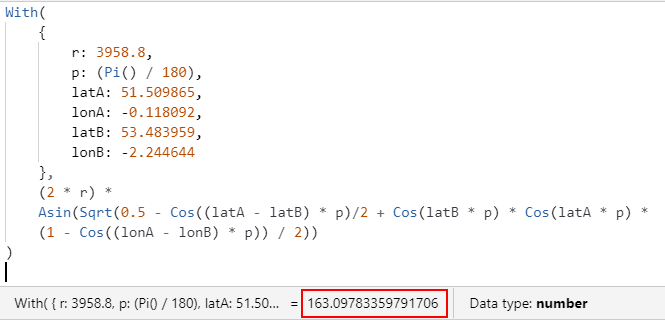
Our formula is based on the hardcoded value of the approximate radius of the earth in kilometres. To use a different unit of measurement, we can substitute the radius value as necessary.

To measure the distance in miles, we can substitute 6371km with the equivilant value in miles, 3958.8 miles. 

//Distance between 2 points in miles
With(
    {
        r: 3958.8,
        p: (Pi() / 180),
        latA: 51.509865,
        lonA: -0.118092,
        latB: 53.483959,
        lonB: -2.244644
    },
    (2 * r) * 
    Asin(Sqrt(0.5 - Cos((latA - latB) * p)/2 + Cos(latB * p) * Cos(latA * p) * 
    (1 - Cos((lonA - lonB) * p)) / 2))
)
This formula produces the verifiable result of 163 miles, as shown beneath.

Conclusion

The Haversine formula enables us to calculate the distance between two points. This post described a how to perform this calculation in Power Apps in both kilometers and miles, including a verification of the result.

Previous
Next
Related posts