Blog

Calculations - What mistakes can happen when we fail to use round brackets correctly in calculations?

What can go wrong when we fail to use brackets correctly in mathematical calculations? This post provides an example.

At a recent event, I had the pleasure to meet mathematician Kyle Evans https://www.kyledevans.com/ Kyle demonstrated a viral mathematical question that circulated a couple of years ago. This provided a good reminder of why it's important to apply parenthesises/brackets correctly to mathematical expressions.

The question is this - what's the answer to the following expression?

8 ÷ 2 x (2 + 2)
What do you think is the answer to this question?

What answers do most people give to this question?

Around half the people think the answer is 16, whilst the other half think it's 1.


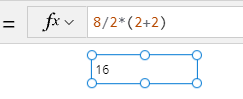
What answer does Power Apps give?

When we carry out this calculation in Power Apps, the result is 16 - which is strictly the correct answer.


Why is there so much confusion?

The reason for this confusion appears to stem from a misunderstanding of how to apply mathematical operations in the correct sequence.

Specifically, schools in the US commonly teach the order of operations using the acronym PEMDAS. This stands for "Parentheses Exponents Multiplication Division Addition Subtraction", and is abbreviated to "please excuse my dear aunt Sally".

However, in the UK, Australia, and other English speaking countries, schools use the acronym BODMAS instead. BODMAS stands for "Brackets Order Division Multiplication Addition Subtraction".

Notice how with PEMDAS, multiplication comes before division whereas with BODMAS, division comes before multiplication. Therefore, someone using the BODMAS acronym can more likely be inclined to perform the calculation like so, which will result in 1.

8 ÷ (2 x (2 + 2))

What's the correct way to apply mathematical orders of operation?

With both PEMDAS and BODMAS, multiplication and division, and addition and subtraction are either/or operations, and this is the point that confuses many.

In other words, the key point is that multiplication and division are identical operations. Addition and subtraction are also identical operations.

  • Division is the same as multiplying a number by a fractional number
  • Subtraction is the same as adding a negative number

Therefore in this example, multiplication does not take precedence over division, and division also does not take precedence over multiplication.

Where an expression contains both multiplication and division, there is equal precedence. In these cases, the order of operation will apply from left to right.

(8 ÷ 2) x (2 + 2)

Conclusion

When building apps, it's very common to construct mathematical expressions that contain a range of operators. We see this commonly in cases where we calculate proportions and percentages. It's important to understand the order of operations to avoid errors. The advice from mathematicians is that a good mathematician will always use parenthesis to help document and to express the intention of an expression, even when they are not necessary.

Finally, we leave on another of Kyle's puzzles. Three app-builders go out for dinner. Each app builder orders a pizza for $10. When the bill arrives, each app builder puts in a $10 bill. The waitress then tells the group - "good news, we have a special offer where we offer 3 pizzas for $25". The waitress leaves and comes back with the change (5 $1 bills). Each app builder takes $1, and they leave the remaining $2 as a tip. Afterwards, the app builders calculate what they've paid. Each app builder has effectively paid $9, which amounts to $27 in total. They left a $2 tip to the waitress, bringing the total to $29. What happened to the remaining $1?
Previous
Next
Related posts